You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Va changes with Weight
- Thread starter LS1 Life
- Start date
CDNPilotDave
Well-Known Member
I had that exact question on my Commercial ride. Although I could spout the party line he explained it as "flickability". The less weight on the airplane, the easier it is to subject the airplane to max G's. I look at it as inertia. When there is more mass contained onboard the greater the tendency to proceed in its original direction. A really lightly loaded airplane can be 'redirected' and thus subject to greater stresses. As gross weight increases, so does Va.
AirmetTango
Well-Known Member
Assume two identical airplanes, say Cessna 172s, traveling at 100 kts. The only difference between the two is that one is heavier than the other. The heavier one needs to generate more lift, because of the greater weight. Since all things are otherwise equal, the only way more lift can be generated for the heavier plane is to fly at a higher angle of attack, or more importantly, closer to the critical angle of attack. Less control deflection is needed to stall the heavy airplane, so it stalls before enough force can be generated to exceed G-loading.
The lighter airplane at the same speed needs less angle of attack, so there is more "room" to move the controls before reaching the critical angle of attack and the forces generated by a control deflection can break the airplane before it has a chance to stall. The only option to stay safe is to slow down (slower Va speed), so the lighter airplane is at a higher angle of attack, and the airplane can stall before it generates enough force to break.
The lighter airplane at the same speed needs less angle of attack, so there is more "room" to move the controls before reaching the critical angle of attack and the forces generated by a control deflection can break the airplane before it has a chance to stall. The only option to stay safe is to slow down (slower Va speed), so the lighter airplane is at a higher angle of attack, and the airplane can stall before it generates enough force to break.
Assume two identical airplanes, say Cessna 172s, traveling at 100 kts. The only difference between the two is that one is heavier than the other. The heavier one needs to generate more lift, because of the greater weight. Since all things are otherwise equal, the only way more lift can be generated for the heavier plane is to fly at a higher angle of attack, or more importantly, closer to the critical angle of attack. Less control deflection is needed to stall the heavy airplane, so it stalls before enough force can be generated to exceed G-loading.
The lighter airplane at the same speed needs less angle of attack, so there is more "room" to move the controls before reaching the critical angle of attack and the forces generated by a control deflection can break the airplane before it has a chance to stall. The only option to stay safe is to slow down (slower Va speed), so the lighter airplane is at a higher angle of attack, and the airplane can stall before it generates enough force to break.
This is a perfect explanation and the reason why. Sorry CDN but inertia really has nothing to do with it and in fact would cause you to think of it back wards.
Assume a heavier aircraft, it has more inertia right? So by the "more inertia" theory it would have a lower Va because it can "over-speed" (a false belief that speed has a bearing on Va, it does not). As you can see this theory leads you in the wrong direction because in fact with an increase in weight there is an increase in Va.
For a practical way to imagine angle of attack increase for weight is to think of a fat water skier and a light water skier at the same speed. The heavier skier will have his ski tips up in the air to sustain the extra weight.
Finally, in your example you are confusing inertia with momentum. Momentum is what would cause it to continue to move in one direction or another, inertia is an objects Resistance to movement.
braunpilot
What day is it?
I just remember it as take the square root of the current wt divided by the max gross weight then multiply that by Va.
SqRoot|(current wt/max gross wt) * Va
SqRoot|(current wt/max gross wt) * Va
Actually inertia is an objects resistance to a change in it's state of motion.Finally, in your example you are confusing inertia with momentum. Momentum is what would cause it to continue to move in one direction or another, inertia is an objects Resistance to movement.
It's an objects resistance to moving if it isn't moving and it's the objects resistance to stopping if it is moving.
-mini
R
Roger, Roger
Guest
That is essentially the explanation that I use.Assume two identical airplanes, say Cessna 172s, traveling at 100 kts. .....
...... The only option to stay safe is to slow down (slower Va speed), so the lighter airplane is at a higher angle of attack, and the airplane can stall before it generates enough force to break.
Actually inertia is an objects resistance to a change in it's state of motion.
It's an objects resistance to moving if it isn't moving and it's the objects resistance to stopping if it is moving.
-mini
Touche (spelling?). My apologies, the rest still remains true.
Sidious
Well-Known Member
That is essentially the explanation that I use.
Me too... Seems to work out pretty well
Dig out a Vg diagram and work it for two different stall speeds. I've attached a crude one, please forgive my lousy photoshop skills.
Basically, since a lighter aircraft stalls at a slower indicated airspeed it will reach it's load limit at a lower airspeed as well, hence Va decreases with as weight decreases.
At speeds higher than Va you'll reach the load limit before the airplane stalls and risk bending something important. At or below Va, the airplane will stall before the load-limit is reached, protecting you from yourself.

Basically, since a lighter aircraft stalls at a slower indicated airspeed it will reach it's load limit at a lower airspeed as well, hence Va decreases with as weight decreases.
At speeds higher than Va you'll reach the load limit before the airplane stalls and risk bending something important. At or below Va, the airplane will stall before the load-limit is reached, protecting you from yourself.

the_dmn8tr
New Member
Rod Machado has a great article about it on the AOPA website. Basically, while it is true that a heavier aircraft is closer to the critical angle of attack, it has more to do with G-Forces imposed.
Remember that a normal category aircraft has a positive limit load factor of 3.8 G's. Two aircraft with different weights have a different airspeed for Va because that airspeed represents the generation of 3.8 G's between the angle of attack and the critical angle of attack. If you fly above Va in turbulent airspeed, you have a lower angle of attack since you are at a higher airspeed. Sudden control deflection would result in more Gs than the aircraft can support, resulting in structural failure. Flying below Va results in a higher angle of attack because of a slower airspeed. Sudden control deflection results in an accelerated stall before high G loads can be imposed.
Remember that a normal category aircraft has a positive limit load factor of 3.8 G's. Two aircraft with different weights have a different airspeed for Va because that airspeed represents the generation of 3.8 G's between the angle of attack and the critical angle of attack. If you fly above Va in turbulent airspeed, you have a lower angle of attack since you are at a higher airspeed. Sudden control deflection would result in more Gs than the aircraft can support, resulting in structural failure. Flying below Va results in a higher angle of attack because of a slower airspeed. Sudden control deflection results in an accelerated stall before high G loads can be imposed.
Attachments
Basically, since a lighter aircraft stalls at a slower indicated airspeed it will reach it's load limit at a lower airspeed as well, hence Va decreases with as weight decreases.
I am at work and cannot address this now, however there is some erroneous thought process here. I will be home later and elaborate talk to you all then.
Edit: from here on added.
The erroneous thought process lies in the bold lettering as noted above is not so much wrong (because it is in fact true), it however completely leaves out the why. First off all v-speeds go down with weight, each for different reasons and just because one goes down for one reason doesn't mean the others have to go down, sure they do, but the reasoning is still different.
Edit: added first why and bolded the second for clarification, I am not argueing they are unrelated. I am saying the reasons for each are unrelated.
For example, the reason why stall goes down is completely unrelated to the reasoning for why Va goes down with weight, for stall we have this:
First it is known that lift must overcome weight to maintain flight.
Now we must know how you determine lift:
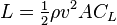
In the above formula L = lift, p = air density, v = velocity, a = area of the wing, and Cl = coefficient of lift found by (Cl = 2 * pi * angle (in radians)).
Now let us assume that aircraft a weights 2000 lbs and b weights 2500 lbs and both stall at 18 degrees and have are the exact same aerodynamically. So we will fly each aircraft at exactly 18 degrees angle of attack maxing our Cl and leave that as a constant, we will also leave density and wing area as a constant. All that is left to adjust the formula to raise or lower the value of L is velocity, this is why stall speed decreases. Since aircraft weighs in at 500 lbs less than aircraft b than aircraft a can maintain sufficient lift (2000lbs) at a slower airspeed than aircraft b w/o exceeding critical angle of attack. Aircraft b to fly at the same speed as aircraft a and get enough lift would have to raise its angle of attack or increase its airspeed, since raising AOA will go past 18 degrees (our critical for this simulation) then aircraft b will stall if it tries to do that.
As for Va that has already been discussed and the above mentioning of it relating to flying at a lower AOA and being further from critical are in fact the reason Va changes with weight. It isn't that it overloads at a lower airspeed and in fact the Vg diagram does nothing to display Va changing with weight, it overloads at a lighter weight at a lower airspeed because it is further from critical angle of attack and because its further from critical AOA that gives you that much more "time" shall we say, to bring the aircraft beyond its load limit. The post above mine is a good example but relates to speed and not weight which can cause some confusion but the idea remains the same. A heavier aircraft will need to fly at a higher angle of attack (see formula and how you find Cl) to maintain enough lift to overcome weight, because this higher AOA is closer to critical Va can be reduced.
An interesting add here that I think all CFIs should know is thie structural limits of an aircraft are based on:
1) Symmetrical loading (pulling in a turn is different then straight and level!) At Va in a turn the outside wing is faster than Va...inside slower...
2) Progressive loading (snap stalls at Va might leave you without a wing)
3) Changes based on materials (not really something a pilot needs to worry about)
tgrayson
New Member
For example, the reason stall goes down is completely unrelated to the reasoning for why Va goes down with weight,
Given that the formula for Va (non-FAA version) is

Maurus
The Great Gazoo
Given that the formula for Va (non-FAA version) is
I'll have to disagree with you. Va (non-FAA version) is simply the stall speed when pulling the load factor limit.,
That's exactly it. Va is a stall speed for your max load factor. Which means Va goes down for the same reason the stall speed goes down with less weight.
Given that the formula for Va (non-FAA version) is
I'll have to disagree with you. Va (non-FAA version) is simply the stall speed when pulling the load factor limit.,
Very true, and like I said later in the post:
The erroneous thought process lies in the bold lettering as noted above is not so much wrong (because it is in fact true), it however completely leaves out the why.
I agreed that the the definition was true, it was the reasoning behind it that fails to give the student or show the examiner the applicants true understanding of the aspects involved. That it is because of a greater distance between normal cruising AOA and critical AOA. By the reasoning given you could simply say then that best glide goes down because stall speed goes down because the weight goes down which proves nothing of a students knowledge as to why it happens. (In this case total drag curves, less lift need = less induced drag and so on...)
Point is the reason can't simply be stall speed dropped because weight dropped therefore Va must drop, that applies across the V speed board and shows zero comprehension of what is going on.
Tgray, where did you find that formula though? It sounds right, seems to work right, and I think I remember seeing it (checked my flight dynamics notes with no luck) and all my flight dynamics books are at work so I will reference them tomorrow.
That's exactly it. Va is a stall speed for your max load factor. Which means Va goes down for the same reason the stall speed goes down with less weight.
The bold is wrong, see my above post. They have the same result, but for different reasons.
major snipping....
The erroneous thought process lies in the bold lettering as noted above is not so much wrong (because it is in fact true), it however completely leaves out the why.
Yeah, that's why I added the "basically" qualifier.
tgrayson
New Member
I agreed that the the definition was true
Well, you disagreed, then agreed, then disagreed again, so it was/is ambiguous as to what point you were trying to make.
The very best presentation of the material is the way the_dmn8tr described it, but both woutlaw and AirmetTango are correct, too. All of these explanations communicate the same truth and are consistent with each other.
No, you cannot say that because best glide is not related to stall speed. Va, however, is.By the reasoning given you could simply say then that best glide goes down because stall speed goes down because the weight goes down
You can derive it from the lift formula. But you can find it the form I used in lots of aerodynamics books. Probably Aerodynamics for Naval Aviators has it....let me check......ok, you'll find it in Chapter 5, page 339.Where did you find that formula though?
Maurus
The Great Gazoo
The bold is wrong, see my above post. They have the same result, but for different reasons.
Funny, since it was correct in my aerodynamics class in which we used Aerodynamics for Naval Aviators as one of our textbooks.
MidlifeFlyer
Well-Known Member
Here's my best shot for comprehending it without a degree in physics.Alright guys, I'm getting way too many ways of describing how and why maneuvering speed changes with weight...
Tryin to find an easier way to explain it so other's can comprehend it.
Give me your best shot, if there's a link or photos you use, add them!
Maneuvering Speed and the "AoA Gap"
The whole idea of maneuvering speed is to lower the distance between your in flight AoA and the critical AoA (the "AoA Gap"), so that in case of an event that closes the gap, you will stall before the G-load becomes too great.
In general the faster you go in level flight, the lower your iAoA and the larger the AoA Gap. In the yellow arc, the AoA Gap is large enough that even an event that doesn't close the Gap can cause those excess G's. And an event that does close the Gap is almost guaranteed to cause structural damage.
This explanation was derived from a number of online and offline sources.
Let's go back to the definition of maneuvering speed. Euphemistically, it's the speed at which an airplane will stall before it breaks due to a gust or abrupt control movement.
Putting it in slightly other terms, it's the speed at which the wings can suddenly go from their existing angle of attack to their critical angle of attack without increasing the load factor (G-force) beyond the aircraft's design limit. For normal category aircraft, that design maximum is 3.8 G.
Let's fill this out with some numbers. We are flying an airplane that stalls at 15º AoA. At it's normal 120 KT cruise, it's AoA is 3º.
What happens if we suddenly change the AoA from 3º to 15º? Because there is (roughly) a one-to-one relationship between increase in AoA and increase in load, we have just increased the ~1-G cruise load on the wings by a factor of 5 G. Too bad we suffered structural damage at 3.8!!
What we're really trying to do to protect ourselves is increase our AoA so that the gap between our AoA and the critical AoA is smaller. How do we do that? We slow down. When we slow down while maintaining level flight, we reduce power and increase pitch, which increases our AoA. So, let's say that flying our hypothetical airplane level at a 90 KTS takes a 5º AoA. Even that small change means that suddenly bridging the AoA gap only involves a 3-G increase, below the 3.8 G damage point.
Why the slower speed for lower weight? Well, in general, a lighter airplane can maintain level flight at a particular airspeed with a lower angle of attack. So the cruise to critical AoA gap is larger at lighter weights. So we need to slow down more to get our cruise AoA where we need it to be to keep the gap manageable.
Similar threads
- Replies
- 104
- Views
- 9K
- Replies
- 45
- Views
- 7K


