Me too, in Haines. Although as I recall it I was hitting the aileron stop.
Xwind Calculation at Airlines
- Thread starter bc2209
- Start date
Cptnchia
Dissatisfied Customer
D
Deleted member 27505
Guest
Crab on final. If you can keep the long axis of the airplane aligned with the runway and the direction of flight, you'll be fine. If in a jet, release the crab and kick the rudder as you put your wheels down. If in an airplane in which you can land in the crab, land in the crab. "Look, Ma. No math!"
Richman
JC’s Resident Curmudgeon
Not even...
30 degrees is .5
45 degrees is .7
60 degrees is .9
Worried about tailwind components? Works the same (past 90 degrees):
120 degrees is .5
135 degrees is .7
150 degrees is .9
Just remember 5/7/9
Not exact, but close enough for a WAG.
Richman
bLizZuE
Calling for engine starts en français
My technique.
flyboy6585
Well-Known Member
I look at my watch...if it is 15 degrees off the runway the xwind is 1/4 or 25% of the velocity, at 30 degrees off it is 1/2 or 50%, at 45 degrees 3/4 or 75% and 60 is the 1/1 of the velocity. If you look at the watch it is the same 15 is 1/4 of the way around the face, 30 is 1/2, 45 is 3/4, and 60 is the whole way around.
That said, in my current jet we just touchdown in a crab.
That said, in my current jet we just touchdown in a crab.
BajtheJino
I'm looking at you.
I never weren't no good at all that fancy book lernin and cipherin, but as a professional aviator isn't it my jorb to extract the maximum performance outta muh airplane er'yday?
Sigh...I wear a digital watch.
Roger Roger
Bottom of the list
This is the best technique I've used.
ppragman
FLIPY FLAPS!
Sigh....
This is why I get frustrated when pilot brag about how little math they know how to do. To be honest, because of this sort of thing, trigonometry was by far the most useful class I took in college in relation to being a pilot for a living. If you were going to take and care about one and only one math class as a pilot - care about trig. It has so many relatively "day to day" applications I don't even know where to begin. The rules of thumb are great (about the only one I ever cared to think about was the 5/7/9 rule as someone mentioned above) and the rules for figuring out a 3° glide slope, but there are quite a few ways that you can use trig in the flight planning process, or even in route - in fact I've done it.
For instance - you're sitting up at FLXXX headed to your destination bored out of your gourd, the GOM/FOM/WOM (whatever OM) says that pilots shall not attempt to land with greater than what's published in the manual, which, let's say is 30KTS. The wind has been steady directionally 50°, but gusting up and down all evening. How do you know you're going to be legal to even try it? Reaching back to high school we remember:
sin Theta = Opposite / Hypotenuse. Well, we know the Theta (that's your angle), the sine of theta - or sin(θ) if you're mathematically inclined - is equal to the ratio of the opposite end of the triangle you've drawn and the hypotenuse. Someone has drawn a really awesome picture of this.
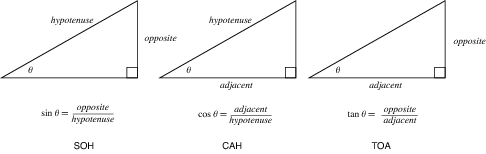
Since you know that the hypotenuse is the wind pointing at you, the "adjacent angle" is going to be your groundspeed, the crosswind component is the "opposite angle." So let's set up the problem:
sin(angle_between_runway_and_wind) = crosswind_component / wind_speed
Recall that we already knew what the max crosswind component we could tolerate was and the wind speed so:
sin(50°) = 30 Knots / wind_speed
So we do some algebra:
sin(50°) = 30kts / wind_speed ----> wind_speed * sin(50°) = 30kts -----> wind_speed = 30kts / sin(50°)
Sweet! You grab your smart phone and plug these numbers into the calculator, "Okay, sine 50 is -.2623...! That can't be right!" You're correct, it isn't right, you need to be using degrees and the calculator is in radians- which if you had taken trig you'd know why, but suffice it to say that you can still use your smartphone's calculator, just make sure it's in degrees and not radians. The one on my iPhone says "rad" over in the left side when it's in radians. YMMY. Anyhow, 30kts / sin(50°) is 39.16kts, or 39kts. If the gusts are above 39 knots, land somewhere else or whatever, be a hero, but if you ball it up know that this is the way the NTSB will figure out what your crosswind component was.
That whole chart above covers other things too. Ever wonder why a 3° glide slope is about 300' / nm? That's why. Ever wonder how VNAV descent profiles get calculated? That's how (among a few other ways) it's done. Trig is insanely useful to know.
This is why I get frustrated when pilot brag about how little math they know how to do. To be honest, because of this sort of thing, trigonometry was by far the most useful class I took in college in relation to being a pilot for a living. If you were going to take and care about one and only one math class as a pilot - care about trig. It has so many relatively "day to day" applications I don't even know where to begin. The rules of thumb are great (about the only one I ever cared to think about was the 5/7/9 rule as someone mentioned above) and the rules for figuring out a 3° glide slope, but there are quite a few ways that you can use trig in the flight planning process, or even in route - in fact I've done it.
For instance - you're sitting up at FLXXX headed to your destination bored out of your gourd, the GOM/FOM/WOM (whatever OM) says that pilots shall not attempt to land with greater than what's published in the manual, which, let's say is 30KTS. The wind has been steady directionally 50°, but gusting up and down all evening. How do you know you're going to be legal to even try it? Reaching back to high school we remember:
sin Theta = Opposite / Hypotenuse. Well, we know the Theta (that's your angle), the sine of theta - or sin(θ) if you're mathematically inclined - is equal to the ratio of the opposite end of the triangle you've drawn and the hypotenuse. Someone has drawn a really awesome picture of this.
Since you know that the hypotenuse is the wind pointing at you, the "adjacent angle" is going to be your groundspeed, the crosswind component is the "opposite angle." So let's set up the problem:
sin(angle_between_runway_and_wind) = crosswind_component / wind_speed
Recall that we already knew what the max crosswind component we could tolerate was and the wind speed so:
sin(50°) = 30 Knots / wind_speed
So we do some algebra:
sin(50°) = 30kts / wind_speed ----> wind_speed * sin(50°) = 30kts -----> wind_speed = 30kts / sin(50°)
Sweet! You grab your smart phone and plug these numbers into the calculator, "Okay, sine 50 is -.2623...! That can't be right!" You're correct, it isn't right, you need to be using degrees and the calculator is in radians- which if you had taken trig you'd know why, but suffice it to say that you can still use your smartphone's calculator, just make sure it's in degrees and not radians. The one on my iPhone says "rad" over in the left side when it's in radians. YMMY. Anyhow, 30kts / sin(50°) is 39.16kts, or 39kts. If the gusts are above 39 knots, land somewhere else or whatever, be a hero, but if you ball it up know that this is the way the NTSB will figure out what your crosswind component was.
That whole chart above covers other things too. Ever wonder why a 3° glide slope is about 300' / nm? That's why. Ever wonder how VNAV descent profiles get calculated? That's how (among a few other ways) it's done. Trig is insanely useful to know.
Cherokee_Cruiser
Bronteroc
I use the WindTrig app.
Sigh....
This is why I get frustrated when pilot brag about how little math they know how to do. To be honest, because of this sort of thing, trigonometry was by far the most useful class I took in college in relation to being a pilot for a living. If you were going to take and care about one and only one math class as a pilot - care about trig. It has so many relatively "day to day" applications I don't even know where to begin. The rules of thumb are great (about the only one I ever cared to think about was the 5/7/9 rule as someone mentioned above) and the rules for figuring out a 3° glide slope, but there are quite a few ways that you can use trig in the flight planning process, or even in route - in fact I've done it.
For instance - you're sitting up at FLXXX headed to your destination bored out of your gourd, the GOM/FOM/WOM (whatever OM) says that pilots shall not attempt to land with greater than what's published in the manual, which, let's say is 30KTS. The wind has been steady directionally 50°, but gusting up and down all evening. How do you know you're going to be legal to even try it? Reaching back to high school we remember:
sin Theta = Opposite / Hypotenuse. Well, we know the Theta (that's your angle), the sine of theta - or sin(θ) if you're mathematically inclined - is equal to the ratio of the opposite end of the triangle you've drawn and the hypotenuse. Someone has drawn a really awesome picture of this.
Since you know that the hypotenuse is the wind pointing at you, the "adjacent angle" is going to be your groundspeed, the crosswind component is the "opposite angle." So let's set up the problem:
sin(angle_between_runway_and_wind) = crosswind_component / wind_speed
Recall that we already knew what the max crosswind component we could tolerate was and the wind speed so:
sin(50°) = 30 Knots / wind_speed
So we do some algebra:
sin(50°) = 30kts / wind_speed ----> wind_speed * sin(50°) = 30kts -----> wind_speed = 30kts / sin(50°)
Sweet! You grab your smart phone and plug these numbers into the calculator, "Okay, sine 50 is -.2623...! That can't be right!" You're correct, it isn't right, you need to be using degrees and the calculator is in radians- which if you had taken trig you'd know why, but suffice it to say that you can still use your smartphone's calculator, just make sure it's in degrees and not radians. The one on my iPhone says "rad" over in the left side when it's in radians. YMMY. Anyhow, 30kts / sin(50°) is 39.16kts, or 39kts. If the gusts are above 39 knots, land somewhere else or whatever, be a hero, but if you ball it up know that this is the way the NTSB will figure out what your crosswind component was.
That whole chart above covers other things too. Ever wonder why a 3° glide slope is about 300' / nm? That's why. Ever wonder how VNAV descent profiles get calculated? That's how (among a few other ways) it's done. Trig is insanely useful to know.
This...I agree. Trig was an extremely useful tool for me in grad school and it's a lot of fun, for me anyway.
Using the above noted metrics are great but it is very important to understand how the trig gets one to the answer.
For me, in a Cessna, getting the atis, I'm already calculating the wind based on the difference between runway heading and wind direction using the 5,7,9 approach. Close enough for me, and It helps me with SA.
For me, in a Cessna, getting the atis, I'm already calculating the wind based on the difference between runway heading and wind direction using the 5,7,9 approach. Close enough for me, and It helps me with SA.
ASpilot2be
Qbicle seat warmer
Hey, that's how I do it.When guys break out the iPad app with wind and runway heading:
Screaming_Emu
Well-Known Member
Nothing good can come from me doing mental math while flying an airplane.
ArcherII
Well-Known Member
Have you ever flown a T-tail Lance? It must be the only modern piston single to dutch-roll...
🦈💜
Well-Known Member
Skagway, oh yea.
Most of the time I've run out of rudder (and it's happened a lot) it's been slipping a taildragger.
-Fox
NovemberEcho
Dergs favorite member
Sigh....
This is why I get frustrated when pilot brag about how little math they know how to do. To be honest, because of this sort of thing, trigonometry was by far the most useful class I took in college in relation to being a pilot for a living. If you were going to take and care about one and only one math class as a pilot - care about trig. It has so many relatively "day to day" applications I don't even know where to begin. The rules of thumb are great (about the only one I ever cared to think about was the 5/7/9 rule as someone mentioned above) and the rules for figuring out a 3° glide slope, but there are quite a few ways that you can use trig in the flight planning process, or even in route - in fact I've done it.
For instance - you're sitting up at FLXXX headed to your destination bored out of your gourd, the GOM/FOM/WOM (whatever OM) says that pilots shall not attempt to land with greater than what's published in the manual, which, let's say is 30KTS. The wind has been steady directionally 50°, but gusting up and down all evening. How do you know you're going to be legal to even try it? Reaching back to high school we remember:
sin Theta = Opposite / Hypotenuse. Well, we know the Theta (that's your angle), the sine of theta - or sin(θ) if you're mathematically inclined - is equal to the ratio of the opposite end of the triangle you've drawn and the hypotenuse. Someone has drawn a really awesome picture of this.
Since you know that the hypotenuse is the wind pointing at you, the "adjacent angle" is going to be your groundspeed, the crosswind component is the "opposite angle." So let's set up the problem:
sin(angle_between_runway_and_wind) = crosswind_component / wind_speed
Recall that we already knew what the max crosswind component we could tolerate was and the wind speed so:
sin(50°) = 30 Knots / wind_speed
So we do some algebra:
sin(50°) = 30kts / wind_speed ----> wind_speed * sin(50°) = 30kts -----> wind_speed = 30kts / sin(50°)
Sweet! You grab your smart phone and plug these numbers into the calculator, "Okay, sine 50 is -.2623...! That can't be right!" You're correct, it isn't right, you need to be using degrees and the calculator is in radians- which if you had taken trig you'd know why, but suffice it to say that you can still use your smartphone's calculator, just make sure it's in degrees and not radians. The one on my iPhone says "rad" over in the left side when it's in radians. YMMY. Anyhow, 30kts / sin(50°) is 39.16kts, or 39kts. If the gusts are above 39 knots, land somewhere else or whatever, be a hero, but if you ball it up know that this is the way the NTSB will figure out what your crosswind component was.
That whole chart above covers other things too. Ever wonder why a 3° glide slope is about 300' / nm? That's why. Ever wonder how VNAV descent profiles get calculated? That's how (among a few other ways) it's done. Trig is insanely useful to know.
Annnnnd this is why I'm a controller and not a pilot. I'm much better at video games than math.