Aerodynamics: Center of Pressure

Adrock

Adrock

Well-Known Member
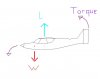
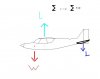
The center of pressure (CP) on a wing is sort of like the center of gravity in that it is the center or concentration of forces. If one could attach a string at the center of gravity and suspend an airplane it would balance. If one attached a string at the station location where the center of pressure exists for a given flight condition (we know CP changes during flight) and an aircraft where suspended by this string the airplane would nose over due to the CG being ahead of the CP. Now visualizing the upward force as this string suspending the aircraft at its CP and the CG (ahead of the CP) as a string pulling down, one can see that the larger the distance (arm/leverage) between the two values the harder the tail has to work to overcome the nose down moment. Given this visualization I find it hard to believe that an aircraft pitches about its CG and not it’s CP. Go ahead guys, where did I go wrong?
 
You have it right, which makes me wonder how come you're having hard time with it. One thing to keep in mind is that the gravity goes directly down through the CG and does not contribute in any way to the pitching up/down rotation. So all that you have to balance, rotation-wise, is the torque created by the wing and the horizontal stabilizer. The arm of the stabilizer is much longer than the wing, so it needs to generate much more lift. Now all this gets you no rotation. To make sure that the airplane is not accelerating up and down, the sum of all these force has to be zero. So the sum of the weight and the downward lift generated by the tail has to be the same as the amount of lift generating by the wing. Does this help?
 
I have always heard all three axes meet at the CG. Because movement is around the axis, movement would be rotating around the CG.
 
That's exactly correct - rotation happens around the CG. I think you're mixing the linear movement along any any of the axises with rotation around them. Pitching up and down is rotation along the lateral axis. What controls if and how much rotation happens is the sum of all the torques, where the torque is force x arm. Since the weight can be considered to go through the CG, its arm is 0 and thus its torque is zero as well.

Try to visualize the airplane as a bicycle wheel. No matter how much you pull it up or down by its axis, the wheel will not start turning. Now imagine that you pushed one of the spokes very close to the axis up - that will be your lift at the CP - it will make the wheel turn. If you wanted to prevent the wheel from turning, you could push on the same spoke but much further away from the axis. You'll need to push much lightly there - that's the force from the tail.

All this does not guarantee that the wheel will not fall up or down - only that it will not turn. To make it stay steady in the air you'll have to make sure that you're pushing on the spoke up hard enough to counteract for both the weight and whatever force you're using to push down at the far end of the spoke.
 
Ah, but torque are cuased not just by weight but by forces (like downforce of a tail) so in a balanced condition in level flight where the tail is offsetting the forward cg the net forces (including tail forces) are zero at the Center of Pressure.
 
p.jpg
 
Yes, that's correct. For the system (airplane) to be in equilibrium, you need the net force to be zero and the net torque to be zero. If Fw is the weight, Fl lift from the wing and Fd the force from the tail and CG is center of gravity, CP center of pressure and CPt center of pressure of the tail, you have:
Fw-Fl+Fd=0=net force on the airplane
Fw x arm - Fl x arm + Fd x arm = Fw x 0 - Fl x |CP-CG| + Fd x |CPt-CG| = 0 = net torque on the airplane
In balanced condition the net force on the airplane is 0. That is not the same thing as saying that the force applied on any point of the airplane is zero - you can have two opposing force with the same magnitude applied at two different points of the airplane. If that's the case, it will still not move. It might rotate though, unless the torque generated by these two forces is 0 too.
So don't forget that torque and force are two different things and both of them need to be made zero for the airplane to be in equilibrium.
 
Yep, saw the picture - it's good. Note how the torque is created only by the lift. The weight is going through the CG and if the lift was not present, the airplane would pitch either way. Now all you need to do to balance the rotation is to add some force that will create the opposite amount of torque.
 
Ok agreed but bear with me here.
Look at my masterpiece picture again
Pretend the lift arrow is a string and grab and pick the plane up
Pretend the weight arrow is a string attached to the bottom of the plane and pull it down

The airplane rotates about a lateral axis that is at the center of pressure NOT CG
obviously the variable force of the tail would balance this system but any pitch changes will occur at the Center of pressure (the string representing the only upward force acting on the system)

GOOD CHAT milski! you working on your CFI too?
 
The CP is the point where the sum of the pressure field acts on the wing. The lift force over the horizontal stab (with its own CP that's not often talked about) zeros out the torqes. Here's milski's words drawn into your picture:
Airplane.jpg
 
Yeah I got that Hook dupin. now looking at this new picture if more force is provided by the tail the airplane will pitch up. It will pitch up about the center of pressure arrow (L)
not the CG (W)

The tail is making up for the torque caused by the difference in location between the Lift and Weight if Lift and Weight were at the same station then no Tail would be needed. thus is the premis behind aft CG loading providing the most efficiency. My original question is about WHERE the rotation occurs
 
Ah, now I see what bothers you. You're concerned about around what point the turning will happen if the system is not balanced? Unfortunately, that's a more complicated question. It can be proven that a free object with some torque applied on it will rotate around its center of gravity (better known as center of mass in physics). The proof is far from trivial and you would not encounter it unless you're taking a higher level physics college course. Generally, the idea is that things rotating around an axis not going through the CG tend to be unbalance and stabilize by the motion becoming a rotation around a different axis, going through the CG.

Part of what confuses you is that the airplane will not do what you expect it to do. Even if you do what you describe, it will still rotate around its CG. A possible way to do this an experiment is to make an wooden or maybe cardboard profile of an airplane. Put it on the table and put a pin in its CG, then attach a string to the CG. If you have the CG correct, pulling the 'airplane' down by the string will not make it rotate.

Now put a pin somewhere behind the first one and pull with a string up - you should be able to notice that airplane will rotate around the first pin. You can try also pulling up and down by the two pins but unless they are well apart from each other, you'll have only a very short period before you start moving the airplane around before rotating it.

Yes, nice chat. Sorry for the 'it can be proven but I'm not going to do it' trick. But it really is not that simple.

Nope, did mine a bit more than 4 years ago. But I finished my renewal just a few days ago! :) How close are you to the checkride?
 
I like the visualization of the pins and I think I get what you are saying: in your example you start with the pin at the CG, ahead of a pin that is aft representing the CP. in that setup the rotation would be around the CG. The problem with this setup is that the tail creates a force that simulates weight and moves the balance point back and a psuedo cg is formed at the center of pressure. If we setup the the experiment as you outlined and then added a string and weight to the tail that was appropriate to balance the system wouldnt the pivot be about the CP?

I thought 1/4 CFI meant you were 1/4 done! I just finished rough drafts of my CFI lesson plans and have not enough contact with the outside world these last couple weeks! Now for perfecting the right seat flying.
 
One has to ask where is the system being supported--whether talking about a fulcrum at a given location under a balance board or the center of pressure supporting the weight of the airplane--the rotaion will occur around where the object is being supported.
 
No, it will still turn around the CG. It can be proven that a free rigid body (meaning that it's not being pushed against some hard point, say a nail in the table) will stabilize its rotation around an axis which goes through the CG. The table experiment is probably not so great, since as soon as the airplane pitches up or down, you start applying forces in other directions (you're not pulling it only up but towards the tail as well) and that make it much more messier. Another few things to try: throw a fairly flat object, some sort of very flat remote control, a soap bar, anything like that - you can notice that it will always turn around the same point, no matter what forces you apply to it.

Another idea - think about a uniform stick. Imagine that you're holding it very close to one of its ends and you are rotating it around that point. As soon as you release it, the rotation point will quickly move from where you held the stick to its center of gravity. Is this one easier to imagine? If not, we can talk more about it. The idea is that whatever the object is, it will tend to rotate around its CG. In the case where there is no pivot point and the rotation starts just by application of a force, it will start immediately around the CG.

1/4 CFI? Where did you see that? I might have meant something by it at some moment by I don't remember even where I wrote it. :)
 
In the airplane case there is no support - the airplane is move in any direction, barring air resistance. Which when applied to the pitch up/down part is negligible.
 
I understand the idea of hammer being thrown center of mass will creat a straight line and the hammer will not appear to rotate at the center of its handle, but you are applying concepts to a free object. Think about a board and a fulcrum. the fulcrum is supporting the board and based on where this support is moved the arms and torques will vary just by virtue of moving the support. An airplane is supported by the center of lift and because of this arms to determine equilibrium are based off of where the object is supported i.e. the center of lift/pressure
 
In the case of the board/fulcrum you have the physical fulcrum preventing the board from rotating around any other point. You actually have a normal force exerted on the board by the fulcrum which will create torque if the opposite sign if you try rotating around any other point. The point of the board right above the fulcrum cannot move up or down unless the board is being bent or broken. That is not true about the CP of the airplane - it can certainly move up and down.
 
Whats the differnce between a board/fulcrum creating a supporting force or a wing creating a supporting force? A force is a force. Whether you consider air "squishy" or not is irrelevant. Is a teeter toter that has a rubber beach ball for a fulcrum going rotate around the fulcrum?
 
You need a huge force to move the point where the board touches the fulcrum down say half an inch - that involves compressing the board and the fulcrum by that half an inch. Moving the CP of the airplane down half an inch involves displacing half an inch of air.

Are we arguing that it will rotate around something different from the CG or are you trying to understand why it rotates around CG?
 
You must log in or register to reply here.
Back
Top