Sigh....
This is why I get frustrated when pilot brag about how little math they know how to do. To be honest, because of this sort of thing, trigonometry was by far the most useful class I took in college in relation to being a pilot for a living. If you were going to take and care about one and only one math class as a pilot - care about trig. It has so many relatively "day to day" applications I don't even know where to begin. The rules of thumb are great (about the only one I ever cared to think about was the 5/7/9 rule as someone mentioned above) and the rules for figuring out a 3° glide slope, but there are quite a few ways that you can use trig in the flight planning process, or even in route - in fact I've done it.
For instance - you're sitting up at FLXXX headed to your destination bored out of your gourd, the GOM/FOM/WOM (whatever OM) says that pilots
shall not attempt to land with greater than what's published in the manual, which, let's say is 30KTS. The wind has been steady directionally 50°, but gusting up and down all evening. How do you know you're going to be legal to even try it? Reaching back to high school we remember:
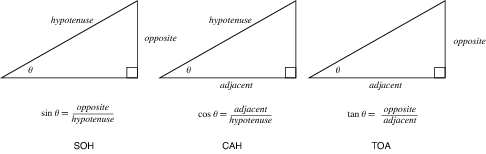
sin Theta = Opposite / Hypotenuse. Well, we know the Theta (that's your angle), the sine of theta - or sin(θ) if you're mathematically inclined - is equal to the ratio of the opposite end of the triangle you've drawn and the hypotenuse. Someone has drawn a really awesome picture of this.
Since you know that the hypotenuse is the wind pointing at you, the "adjacent angle" is going to be your groundspeed, the crosswind component is the "opposite angle." So let's set up the problem:
sin(angle_between_runway_and_wind) = crosswind_component / wind_speed
Recall that we already knew what the max crosswind component we could tolerate was and the wind speed so:
sin(50°) = 30 Knots / wind_speed
So we do some algebra:
sin(50°) = 30kts / wind_speed ----> wind_speed * sin(50°) = 30kts -----> wind_speed = 30kts / sin(50°)
Sweet! You grab your smart phone and plug these numbers into the calculator, "Okay, sine 50 is -.2623...! That can't be right!" You're correct, it isn't right, you need to be using degrees and the calculator is in radians- which if you had taken trig you'd know why, but suffice it to say that you can still use your smartphone's calculator, just make sure it's in degrees and not radians. The one on my iPhone says "rad" over in the left side when it's in radians. YMMY. Anyhow, 30kts / sin(50°) is 39.16kts, or 39kts. If the gusts are above 39 knots, land somewhere else or whatever, be a hero, but if you ball it up know that this is the way the NTSB will figure out what your crosswind component was.
That whole chart above covers other things too. Ever wonder why a 3° glide slope is about 300' / nm? That's why. Ever wonder
how VNAV descent profiles get calculated? That's how (among a few other ways) it's done. Trig is insanely useful to know.