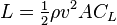induced drag

[clestudentpilot]

I'm sorry if this has been answered before, but I was unable to find it doing a search. Also, this may be something incredibly simple I'm missing, so here it goes. If lift increases as airspeed increases, and induced drag is a direct result of lift, why does induced drag decrease as airspeed increases? I have seen some of the graphs depicting total drag increases, as does parasitic drag, but I don't understand why induced drag would decrease. Any help in understanding this would be helpful. Also, sometimes I tend to act stupid (well, most of the time), so I'm hoping no one uses any of those complex equations I've found online, which do nothing to help me understand haha

 

[tgrayson]

If lift increases as airspeed increases, and induced drag is a direct result of lift, why does induced drag decrease as airspeed increases?

The reason you find this confusing is that most of the literature takes valid concepts out of context.

Yes, according to the lift formula, lift increases as airspeed increases, but the lift formula doesn't tell the whole story. We generally don't have the luxury of increasing airspeed while keeping the other variables the same; in fact, we control airspeed in equilibrium flight by changing our lift coefficient (CL), which is part of the lift equation, and the airspeed will change to whatever velocity is necessary in order to keep Lift = Weight. The point is that in unaccelerated flight, the quantity of lift is always the same, so faster airplanes don't have more lift; rather, they have the same lift as slow airplanes.

 

[Matt13C]

The reason you find this confusing is that most of the literature takes valid concepts out of context.

Yes, according to the lift formula, lift increases as airspeed increases, but the lift formula doesn't tell the whole story. We generally don't have the luxury of increasing airspeed while keeping the other variables the same; in fact, we control airspeed in equilibrium flight by changing our lift coefficient (CL), which is part of the lift equation, and the airspeed will change to whatever velocity is necessary in order to keep Lift = Weight. The point is that in unaccelerated flight, the quantity of lift is always the same, so faster airplanes don't have more lift; rather, they have the same lift as slow airplanes.

If I wanted to put this into laymen terms, say if explaining it to a new PPL student if I instruct, is it acceptable and more importantly accurate to say: In a given configuration, if your airspeed increases parasite drag will increase due to more friction over pieces sticking off the airplane, struts, tires and the plane itself. While induced drag decreases because as you go faster you require less angle of attack, which reduces the pressure differential from teh top of the wing and the bottom of the wing, which decreases wing tip vortexes that are responsible for induced drag?

 

[tgrayson]

If I wanted to put this into laymen terms...

Yes, except that the pressure differential needs to remain constant because lift needs to remain constant.

 

[Holocene]

I'm sorry if this has been answered before, but I was unable to find it doing a search. Also, this may be something incredibly simple I'm missing, so here it goes. If lift increases as airspeed increases, and induced drag is a direct result of lift, why does induced drag decrease as airspeed increases? I have seen some of the graphs depicting total drag increases, as does parasitic drag, but I don't understand why induced drag would decrease. Any help in understanding this would be helpful. Also, sometimes I tend to act stupid (well, most of the time), so I'm hoping no one uses any of those complex equations I've found online, which do nothing to help me understand haha

Increasing airspeed in level flight equates to a decrease in the angle of attack. What this really means, in very simple terms, is that less of the wings underside is dirrectly exposed to the relative wind. Essentially, there aren't as many air molecules hitting the wing at low angles of attack. Thus, induced drag is decreased.

 

[7700]

Wing tip vortices are responsible for induced drag; wing tip vortices are stronger behind airfoils which are flying slower and at higher angles of attack, therefore your induced drag is greater.

 

[shdw]

If lift increases as airspeed increases, and induced drag is a direct result of lift, why does induced drag decrease as airspeed increases?

Because induced drag doesn't increase because lift increases. It is a horrible definition and really screws with a pilots head IMO. Follow through the blow information, maybe a different view will present new information:


Basic Information:

1. For simplicity, assume lift always equals weight.
   
2. Second:
   
   
   
3. Let us rewrite this in words: Lift = 1/2 * air density * velocity squared * wing area * coefficient of lift
   
4. Coefficient of lift is directly effected by the wings angle of attack (AOA). So really, we can replace, for simplicity not accuracy, coefficient of lift with AOA and get: Lift = 1/2 * air density * velocity squared * wing area * angle of attack
   
5. One final step, what can we, as the pilot, change in this formula? We can change AOA and velocity. The rest of the formula isn't really relevant to us. So, we can further simplify this to help the pilot see the relationship between AOA, speed, and lift giving us:
   
   Lift = Speed * AOA

Example:

Remember, since lift always equals weight, we can assume lift is always the same. For example, assume lift is 2,000, speed is 200 and thus AOA is 10.

2000 pounds lift = 200 knots * 10 degrees AOA

Let us change AOA from 10 to 12:

2000 pounds lift = 167 knots * 12 degrees AOA

Hopefully you can clearly see that lift isn't changing, but AOA and airspeed are in constant conflict. They are in search of a balancing point where lift will equal weight.



Apply to Drag Curve:

Redraw this on a piece of paper. On the bottom put 0 on the left and 150 on the right. Draw an arrow from 0 to 150 and mark it airspeed. Below that line, on the left side put 17 degrees and on the right put 1 degree, draw an arrow from the 1 to the 17 and mark it AOA. What it depicts is that as airspeed goes up, angle of attack is going down and thus lift is remaining the same. This is exactly what we showed in the above example section.



Induced Drag Redefined: Induced drag increases when AOA increases. In other words, induced drag varies directly with AOA.



Tgray: I know you haven't been entirely sure of my use of Lift = Speed * AOA or how I work with coefficient of lift in the lift formula. That said, now that you see it applied here what are your thoughts? Thanks.

 

[Matt13C]

Yes, except that the pressure differential needs to remain constant because lift needs to remain constant.

True. So what is the cause for the reduction in wing tip vortex strength? Is it simply as AoA decreases it is harder for air to spill over the top?

 

[tgrayson]

True. So what is the cause for the reduction in wing tip vortex strength? Is it simply as AoA decreases it is harder for air to spill over the top?

That is an excellent question. I'm not sure that I've ever seen that directly addressed in my books; usually they describe how the phenomenon works, and then present the equation that shows how it varies with lift coefficient. I'll have to review the literature and see how that equation is derived. The increased strength of the vortices may be caused by the larger incremement in velocity of the air over the wings necessary at high AoA to provide the same pressure differential.

 

[shdw]

The increased strength of the vortices may be caused by the larger incremement in velocity of the air over the wings necessary at high AoA to provide the same pressure differential.

I've never come across this question, but it is a good one. I wouldn't know where to begin, so I'll leave the research here to you. However, I wonder if tip vortice development has a factor of time involved. If so, aircraft speed would play a factor in development. In other words, less speed equals more time for air below the wing to mix with air above the wing to create the vortex.

 

[tgrayson]

If so, aircraft speed would play a factor in development.

Not likely; otherwise, TAS would be in the equation.

 

[shdw]

Not likely; otherwise, TAS would be in the equation.

Induced drag is a function of dynamic pressure and dynamic pressure is a function of velocity. OTOH after reviewing the formula again it appears an increase in velocity increases induced drag if all other items are held constant. So, my assumption looks to be wrong anyway.

 

[Matt13C]

Induced drag is a function of dynamic pressure and dynamic pressure is a function of velocity. OTOH after reviewing the formula again it appears an increase in velocity increases induced drag if all other items are held constant. So, my assumption looks to be wrong anyway.

If you increase velocity, isnt it impossible to hold everything else constant for a particular airplane? So in a specific airplane, in a set configuration, increasing velocity would only decrease induced drag. Correct?

 

[tgrayson]

If you increase velocity, isnt it impossible to hold everything else constant for a particular airplane? So in a specific airplane, in a set configuration, increasing velocity would only decrease induced drag. Correct?

Yes, but it does time some amount of time for equilbrium to be established. If you cram the throttle forward, you'll see some increase in airspeed until the aircraft has time to pitch itself up and thus reestablish the trimmed airspeed. During that non-equilibrium situation, induced drag will go up as a quantity even if the AoA doesn't change.

 

[tgrayson]

Induced drag is a function of dynamic pressure and dynamic pressure is a function of velocity.

Well, yes, but the induced drag coefficient is independent of those things, and that's what determines the shape of the induced drag curve. It's directly proportional to the lift coefficient^2.

 

[shdw]

that's what determines the shape of the induced drag curve.

Is it the curve we are concerned with though? I thought these curves use coefficients for plotting simplicity, not accuracy. It would seem logical that if we wish to understand induced drag we'd look at all factors involved. Is my thinking flawed?

 

[tgrayson]

Is it the curve we are concerned with though? I thought these curves use coefficients for plotting simplicity, not accuracy.

It depends on what you want to know. Coefficients aren't used for simplicity, they're used because that data is independent of velocity, air density, and wing area. That way you can take those numbers and rehydrate them with the proper environmental and aircraft parameters to get the actual aerodynamic forces. If you merely presented drag, the data would be useless for any purpose except for the particular conditions under which they were recorded.

 

[shdw]

That way you can take those numbers and rehydrate them with the proper environmental and aircraft parameters to get the actual aerodynamic forces.

In other words, for simplicity.

On the actual topic, the question concerns the induced drag of a moving airfoil. It would seem inaccurate to claim velocity constant or ignore it. Aren't we attempting to understand what individual effect causes tip vortice strength to change?

Sorry, I'm not attempting to be difficult. I really don't understand how you can eliminate a variable in this case. I realize most of science is about setting the majority of the variables constant so you can understand how changing one variable effects the outcome of the grand design. (Matt, this is what I did earlier post that you asked about. More on that in a second.)

In this case, I'd be curious to understand velocities impact on vortex strength because it seems important to me. Why is it unimportant? This is what I'm looking to understand. Thanks for the patients tgray.

Yes, but it does time some amount of time for equilbrium to be established. If you cram the throttle forward, you'll see some increase in airspeed until the aircraft has time to pitch itself up and thus reestablish the trimmed airspeed. During that non-equilibrium situation, induced drag will go up as a quantity even if the AoA doesn't change.

This was in response to me holding all variables constant in a formula so I could better understand velocities impact on induced drag. When you look at these formula's, the process I used there is common place in the scientific world. Here, from a book tgray recommended I buy to better learn physics (University Physics):

"As a first step in dealing with a problem of nature it is often necessary to idealize the situation and to make simplifying assumptions concerning the process."

They later go on to discuss the importance of determining conditions of equilibrium as the first, most important step. However, that is for a later discussion. The point here is; we can set every letter in any formula constant to "idealize the situation" so we can better understand how manipulating each variable will effects the aircraft.

For example, you can find every formula where velocity is present. From there you can hold every variable constant in every formula except velocity. We can simply work with lift, having 2 variables in that formula that will readily change: lift coefficient (by changing AOA) and velocity (airspeed).

The rest: lift, wing area, and air density, will remain relatively constant and can be ignored. Since lift can always be simplified to equal weight, as a condition of equilibrium, we can rewrite the lift formula for AOA and velocity:

AOA = 1 / 0.5 * Weight
or
Weight = 1 / 0.5 * AOA

Remember, wing area and air density are constant, so why clutter the formula. Also, lift is constant so I set lift equal to '1' which is why there is a '1' in this formula. Leave them out and only work with things that change, it is simpler. Do you think the formula's we are using include all variables?

Finally, add weight to the first formula there and what happens to AOA? Performing similar processes on other formulai can give similar insights. Furthermore, it leaves no question as to the true answer to "what controls what." It isn't a debatable question in the scientific world.

 

[tgrayson]

In this case, I'd be curious to understand velocities impact on vortex strength because it seems important to me. Why is it unimportant?

Because you need to make a distinction between two different concepts: magnitude and shape. The shape of the induced drag curve is defined by the induced drag coefficient equation and the only variable is the lift coefficient squared. That makes the induced drag curve parabolic and makes induced drag low at high airspeeds and high at low airspeeds.

In the end, to know the magnitude of induced drag, you will need to know the velocity.

 

[Matt13C]

Is velocity the same as speed with speed being time*distance? If thats the case, then is it accurate to say that while at slow speeds and higher AoA, the wing has more time to impart a spin, spillage, on the air going from under to above the wing, increasing the strength of the vortex, more torque?, thus increasing induced drag. As velocity increases and AoA decreases, while the same volume of air is spilling, the wing has less time to impart a spin, less torque more horsepower?, on it so it comes off in a much tighter spin resulting in less induced drag?