AOPA Rod Machado article

[MikeD]

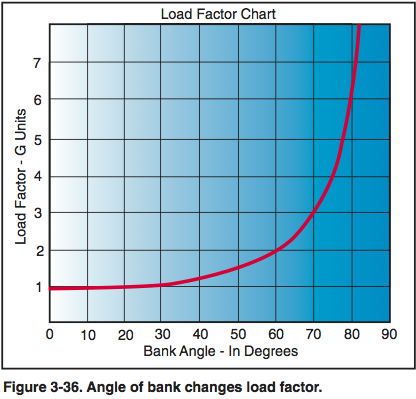
Yes. The bolded portion of the following equation tgray posted is calculating the weight being supported by drag.

G force in a descending turn = cos(descent angle) / cos(bank angle)

If this:

is over your head then I suggest stopping by your local middle school. I'm certain 90 percent of them could set you straight. I know 8th grade algebra class covers what we discussed in this thread, less the use of the trigonometry term cosine.

Keep in mind that the limiting factor is rarely ones ability comprehend. I'm certain, in this and many other cases, that this includes yourself.

.

My issue is that there is no practical application for this in the cockpit in any sort of exacting manner, just in a general manner. For one, even if I had a G meter like I did in fighters, I can't see 1.97. And two, that equation is a mere snapshot of one second of a particular portion of the maneuver.....since flying is dynamic and constantly changing, I can't maintain any parameter rock-solid to that degree for any long period of time, so that 1.97 is only accurate if everything is the same throughout. Academically, its good for teaching a general "hey, this basically whats going on"; but for me it's only practical application is as a rough reference at best, since public math while airborne isn't always the best idea in some circles.

is over your head then I suggest stopping by your local middle school. I'm certain 90 percent of them could set you straight. I know 8th grade algebra class covers what we discussed in this thread, less the use of the trigonometry term cosine.
.

That kind of condscending attitude isnt going to score you many points around here.......well, maybe with the Thurston Howell crowd.

Think about the difference between "need to know" information; and "nice to know" information. As there is a difference.

 

[mshunter]

is over your head then I suggest stopping by your local middle school. I'm certain 90 percent of them could set you straight. I know 8th grade algebra class covers what we discussed in this thread, less the use of the trigonometry term cosine.

Keep in mind that the limiting factor is rarely ones ability comprehend. I'm certain, in this and many other cases, that this includes yourself.

I haven't done that level of math since high school(almost 15 years now), so, disuse comes to mind real quick. I also never had to use that level of math to get through any of my certificates, I don't think. But, you still shouldn't need to teach any math to anyone getting a pilots license. I never had to. I was capable of showing them a graphical representation in textbooks to get the point across, or using basic math to figure things out. Please, save the "go back to middle school" comments. This is no place for them. We don't need to go down that road again my friend. My point still stands. There is no use for your average student using these math calculations. It's un-important. You can use this graph right here to tell them all about load factor.

And then correlate it to this picture:

See how simple that was...............

Best part is, my simple mind understands it. Now all you have to do is get in the airplane with said student, roll in a 45 deg bank and correlate the chart to the feel. then 60, then 90 if the airplane is capable.

 

[swisspilot]

But I have a hard time believing that our modern, GPS equipped, tricycle gear aircraft are actually making us *less* safe than the alternative.

speaking of TAAs they do have a way better safety record then other, more traditional planes, the only higher number of accidents the TAAs have are ADM related to weather.

 

[TwoTwoLeft]

Think about the difference between "need to know" information; and "nice to know" information. As there is a difference.

You hit the nail on the head right there.

 

[shdw]

My issue is that there is no practical application for this in the cockpit.

A quick recap: This discussion has been over whether or not a stabilized, level, 60 degree bank turn has a different g-force than a stabilized descending/climbing one. What the final numbers gave us was that, for typical operations (10 degree or less climb/descent), a 60 degree bank turn is always 2g.

Math was used merely as proof.

I already gave the practical application for such knowledge, though it seems like ages ago at this point so I'll quote it for reference:

This fundamental concept is the key, in my opinion, to teaching climbing and descending turns. Once the student can feel and accurately fly a 30 degree banked, level turn, they can do it from any starting pitch attitude. Simply pitch to a desired attitude and execute a normal level turn. Control pressure and kinesthetic feel will be identical to any level turn. The only change is to the visual picture.

It can also shed light on why a student who enters a steep turn in a slight descent will, without instrument reference, likely fly a perfectly stable descending steep turn. Once the descent has started, if they pull to 2G to fly a typical level turn they will remain in that descent. They must pull more than 2G to bring the nose back up, and/or reduce the bank angle.

 

[shdw]

Please, save the "go back to middle school" comments. This is no place for them. We don't need to go down that road again my friend.

Well, to be fair, I didn't say you should go back. I only said to visit.

It wasn't called for either way though. The basic point was only that the math doesn't exceed the comprehension level of what we expect from a 12 year old. In other words, it isn't that you can't understand it.

My point still stands. There is no use for your average student using these math calculations.

I don't think anyone here said you should be able to do these calculations. Did we? No, I'm not trying to be a wise ass, I really don't recall it being said and I'm to lazy to reread 150 posts.

However, the math was used, successfully I think we can agree, to prove that typical descending turns will exhibit the exact same g-forces as level turns. I mean sure the level 60 degree turn is 2g and the descending (90 kts @ 1500fpm or a 9 degree descent angle) 60 degree turn is 1.97. Really though, I don't think any normal pilot would notice a difference between the two.

 

[MikeD]

A quick recap: This discussion has been over whether or not a stabilized, level, 60 degree bank turn has a different g-force than a stabilized descending/climbing one. What the final numbers gave us was that, for typical operations (10 degree or less climb/descent), a 60 degree bank turn is always 2g.

Math was used merely as proof.

I already gave the practical application for such knowledge, though it seems like ages ago at this point so I'll quote it for reference.

And thats fair. Just remember to keep it simple as the KISS principle states.

 

[z987k]

A quick recap: This discussion has been over whether or not a stabilized, level, 60 degree bank turn has a different g-force than a stabilized descending/climbing one. What the final numbers gave us was that, for typical operations (10 degree or less climb/descent), a 60 degree bank turn is always 2g.

Math was used merely as proof.

I already gave the practical application for such knowledge, though it seems like ages ago at this point so I'll quote it for reference:



It can also shed light on why a student who enters a steep turn in a slight descent will, without instrument reference, likely fly a perfectly stable descending steep turn. Once the descent has started, if they pull to 2G to fly a typical level turn they will remain in that descent. They must pull more than 2G to bring the nose back up, and/or reduce the bank angle.

I think thats the thing... the ones of us arguing against are arguing something different entirely. None of us say a 60* bank won't eventually become 2G's, but to an earlier point about acro and going to 60 and beyond... I think those of us arguing that point know from experience you can roll quite steep with a steep descent angle and eventually roll out without ever coming close to 2G's. This is not a short amount of time either. So in short, yes a Cessna(182, 206, 208) is very capable of what some would consider mild acro without any ill effects whatsoever. In fact you can do it day in day out for years.

 

[shdw]

And thats fair. Just remember to keep it simple as the KISS principle states.

But if the student understands what I say I won't sound as smart...

 

[MikeD]

But if the student understands what I say I won't sound as smart...

Good one! Well played. :clap:

 

[TwoTwoLeft]

What would the numbers look like at somewhere close to redline, idle thrust, and a pegged (or greater) VSI?

My calculator broke so I had to go out and try it! Rolled left & right, no load because bank angle doesn't exist when you're vertical. Before I pulled I was indicating 130kts that translates to a little more than 12,000fpm descent. I pulled for 5Gs, since 130 is my corner speed so I don't accelerate through Vne.

 

[tgrayson]

What would the numbers look like at somewhere close to redline, idle thrust, and a pegged (or greater) VSI?

No real idea, since the vertical speed pegs out in the 1500-2000 fpm in the light airplanes. For such a high airspeed, the vertical speed would have to be very high to compensate. The formula is

angle of descent = arctan(fpm/(knots*6076/60))
​

To verify the forumla, plug in a descent rate of 474 fpm and 90 knots, which should give a 3 degree glideslope. (I get 2.977). Low airspeeds and high descent rate maximize the descent angle.

In a spin, for instance, Kershner says the descent rate can be in the order of 6,000 fpm. At 40 knots, that descent angle would be almost 56 degrees! I'm not sure the calculation is meaningful in this flight regime, but a 60 degree bank would only pull 1.1 g's.

 

[tgrayson]

A wing will stall when the lift is no longer sufficient to counter the LOAD imposed on it.

That definition doesn't make sense, because it's the lift that creates the load in the first place. Load factor = Lift/Weight.

 

[tgrayson]

According to the internet, it's Economics.

I have a BS in Computer Science and Economics. But none of the math I have ever posted is beyond high school level. Anyone who finds that intimidating ought to be not a little embarrassed, rather than chastising me for it. Maybe this is why US students recently ranked 25th in the world in math ability?

 

[tgrayson]

when am I going to bust out my clculator in flight and do this

This has got to be the most absurd critique that continually crops up in so many discussions; its sole purpose seems to be to excuse laziness in pursuing knowledge. No, you don't use this information in the cockpit, you use this on the ground to better understand airplanes so that you can optimize your decision-making once you get in the air. You never know what bit of knowledge might come to your aid some day, and a professional ought to devote his life to gaining as much knowledge about his profession as he can, rather than coasting on what his private pilot instructor taught him in the dozen hours of ground school.

While this sort of discussion clearly doesn't interest you, since you have said so over and over and over, it does interest quite a lot of people, most of whom only read the discussions and don't participate.

 

[SteveC]

No real idea, since the vertical speed pegs out in the 1500-2000 fpm in the light airplanes. For such a high airspeed, the vertical speed would have to be very high to compensate. The formula is

angle of descent = arctan(fpm/(knots*6076/60))
​

To verify the forumla, plug in a descent rate of 474 fpm and 90 knots, which should give a 3 degree glideslope. (I get 2.977). Low airspeeds and high descent rate maximize the descent angle.

In a spin, for instance, Kershner says the descent rate can be in the order of 6,000 fpm. At 40 knots, that descent angle would be almost 56 degrees! I'm not sure the calculation is meaningful in this flight regime, but a 60 degree bank would only pull 1.1 g's.

Maybe I'm not asking the question properly.

What I'm trying to get at is the example given a few times earlier in the thread where guys were (presumably) talking about steep, idle descents after dropping jumpers. I was curious because my (very limited) experience with steep bank angle descents (such as decompression emergency descents in the sim) would lead me to believe that some configurations can lead to a relatively low-G event.

If I understand correctly (debatable, as always), your contention appears to be that this (approx. 1 G, 60 degree bank, descending turn) is a momentary situation and would eventually resolve into an approximately 2-G loading. So, what I'm getting at is; can a jump plane descend at a relatively high bank angle and stabilize at a load substantially closer to 1 G than to 2 G's, given a relatively high descent rate and/or airspeed?

 

[TwoTwoLeft]

That definition doesn't make sense, because it's the lift that creates the load in the first place. Load factor = Lift/Weight.

A wing that its stalled still produces SOME lift.

 

[tgrayson]

So, what I'm getting at is; can a jump plane descend at a relatively high bank angle and stabilize at a load substantially closer to 1 G than to 2 G's, given a relatively high descent rate and/or airspeed?

Yes, but it would require an increasing vertical acceleration downward, which would indicate that the vertical forces weren't in equilibrium. You'd do this by rolling into a bank and continually pushing the yoke forward to neutralize any lift increase that would otherwise occur due to an airspeed increase. This is what I'd do if I needed to be on the ground in a hurry. I'm not sure I'd call this stabilized, though, but I guess that depends on the definition.

Is that what you do in the sim?

 

[tgrayson]

A wing that its stalled still produces SOME lift.

I know it does, but it doesn't help that definition make sense. ;-)

Note that a stalled airplane descends not because it lacks lift, but because it lacks the thrust to overcome the drag of the stalled wing. With enough thrust, it would still achieve level flight, assuming lateral control could be maintained.

 

[SteveC]

Yes, but it would require an increasing vertical acceleration downward, which would indicate that the vertical forces weren't in equilibrium. You'd do this by rolling into a bank and continually pushing the yoke forward to neutralize any lift increase that would otherwise occur due to an airspeed increase. This is what I'd do if I needed to be on the ground in a hurry. I'm not sure I'd call this stabilized, though, but I guess that depends on the definition.

Is that what you do in the sim?

That description sounds accurate to me, but there's often so much other stuff going on during those demonstrations that it can be difficult to recall all the details. I do know that I was adjusting trim as the speed built in order to keep the descent rate high ("neutralizing the lift increase" as you put it). I recall reaching a stabilized configuration with lots of drag (spoilers, sometimes gear and/or flaps depending upon the specific aircraft) and airspeed up near red-line, but I don't honestly remember if we kept all of the bank angle in or just used that to get the downhill movement started quicker, and then rolled to a lower bank angle later in the descent to stabilize at max airspeed. I'm pretty sure that we didn't experience any G-loads substantially higher than 1 until pulling out of the dive at the bottom of the descent. (As an aside, I also know that rolling into a fairly steep bank allowed us to get going downhill fairly quickly without having to unload much below 1 G either. Gotta keep the pax comfortable while they're struggling to get their masks on you know.)

As a follow-up question, is it possible that an aircraft such as a 182 would eventually stop accelerating due to the increased drag as airspeed increased? If it is, is it also possible to determine if that final stabilized speed could reasonably be within airframe limitations?