Steep Gliding Turn Principles

OneNineHundy

OneNineHundy

Well-Known Member
Hi there, I am shortly going to be doing my instructor rating. I am stuck on compiling a brief on the principles involved in a steep gliding turn.

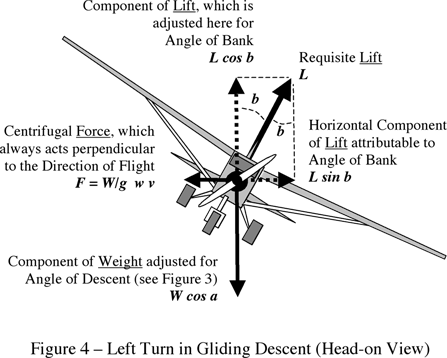
Should I start off by explaining the forces in a level steep turn and then go onto the steep gliding turn? Obviously since the aircraft is descending lift must be less than weight, how would you draw these forces. And since the aircraft is descending do you still require an increase in lift? I think yes because to create the centripetal force you need to incline the increased lift vector, however since you are descending the vertical component of lift is less than weight?

If you could possible give an explanation on how you would deliver the brief, explain the principles, or possibly give a link to a website that might explain it. All the briefs I have seen I don't believe are any good, and the explanations I have received I dont really understand.

Thanks in advance.
 
Thanks Mojo,

I understand the principles of the level steep turn and straight descent it is just difficult to explain the two combined.
 
How about this?

Full link: http://niquette.com/puzzles/revcrses.htm

Figure 4 depicts the situation postulated in the Pilot's Nightmare puzzle -- a gliding turn. As in Figure 2, we have made a strategic choice for our vantage point. Our head-on view this time, though, is looking "uphill" along the descending direction of flight. Thus, neither D nor W sin a (the dead-stick replacement for T) can be "seen" in Figure 4.



revcrs4.gif
[SIZE=+1]In place of W, which always acts downward vertically, Figure 4 shows W cos a, which acts downward perpendicular to the wings asderived in Figure 3. The Lift vector L, which acts perpendicular to the wings, is shown to have a requisite value L = W cos a / cos b. That's what it takes to keep the plane aloft. You will notice that whenever b > a, cos b < cos a, and L > W much as we saw in Figure 2.[/SIZE]
[SIZE=+1]Gliding, say, at Angle of Descent a = 6[/SIZE][SIZE=-1]o[/SIZE][SIZE=+1] and at an Angle of Bank b = 50[/SIZE][SIZE=-1]o[/SIZE][SIZE=+1], the requisite Lift L = 1.5 W. The wings are carrying about half again the gross weight of the airplane, which raises the question, how does the pilot increase the value of L? Answer: increase airspeed, of course. But how much?[/SIZE]​
[SIZE=+1]As described above, L increases according as the square of v. To compensate for banking, we observe that the requisite Lift must be increased from its straight-flight value, L = W cos a, by a ratio that looks like this: (W cos a) / (W cos a cos b) or more simply 1 / cos b. Airspeed, then must be increased from its straight-flight value v[/SIZE][SIZE=-1]0[/SIZE][SIZE=+1] by a ratio that looks like this: v[/SIZE][SIZE=-1]2[/SIZE][SIZE=+1] / v[/SIZE][SIZE=-1]02[/SIZE][SIZE=+1]. Thus, for a gliding turn, the requisite airspeed will be given by v = v[/SIZE][SIZE=-1]0[/SIZE][SIZE=+1] (1 / cos b)[/SIZE][SIZE=-1]1/2 [/SIZE][SIZE=+1](feet per second). Hmm, this determination turns out to be independent of the Angle of Descent a as well as W (a counter-intuitive reality, wouldn't you say?).[/SIZE]
Click to expand...
 
nosehair said:
No disrespect intended to anyone, but if I were a potential student and you were using this to explain gliding turns to me, I would excuse myself with a 'horrendous headache'...
Click to expand...

Well, he is asking for a pretty advanced explanation about it. It is his job to read it and break it down for whatever level he is teaching. Most of it is over my head as well, but you can get the general idea.
 
<Moved thread. Couldn't decide between CFI Corner and Technical, so I flipped a coin. Technical Talk won.>
 
http://niquette.com/puzzles/revcrses.htm

Somewhere in that link it talks about how you might as well just roll it into a 75 degree bank. Then it said if you do that you're going to be pulling in excess of 4 Gs. Now I agree that you'd be pulling 4 Gs if you maintained your altitude, but if you instead maintained your airspeed....well, you'd lose a ton of altitude and would have no significant Gs at all....maybe I'm missing something though.
 
OneNineHundy said:
Obviously since the aircraft is descending lift must be less than weight, how would you draw these forces.
Click to expand...

That's only obvious if you assume that descents are caused by a loss of lift. They are not. They are caused by a lack of thrust.

Now, it so happens that when an aircraft descends, the aircraft's drag helps support the weight of the aircraft, so less lift is needed. But that's more an effect of the descent than the cause.

A further illustration is that in a climb, lift is also less than weight, because thrust supports part of the weight of the aircraft too.

Note that these reductions in lift are very small. For instance, in a straight gliding flight, you may be descending at a 6 degree angle. This equates to a quantity of lift of cos(descent angle) = .996, meaning that lift is 99.6% of level flight lift.

<<And since the aircraft is descending do you still require an increase in lift? I think yes because to create the centripetal force you need to incline the increased lift vector, >>

Yes. A gliding turn is essentially the same as a level turn.
 
dpilot83 said:
but if you instead maintained your airspeed....well, you'd lose a ton of altitude and would have no significant Gs at all....maybe I'm missing something though.
Click to expand...

A steady, 60 degree banked pulls pretty close to 2g's in level flight, descents, and climbs.

Now, you can temporarily unload a turn by allowing the airspeed to increase, but as the airspeed picks up, so does the load factor.

(Note that there is a *small* reduction in load factor during a descent/climb, because drag & thrust help support the aircraft's weight, but it's not enough to help matters.)
 
I think I have got my head around it. I will start ff by revising the forces in the steep turn. Lift is proportional to AoA and airspeed. In a level glide you fly at the speed for the best Lift to drag ratio. Therefore to increase the lift force which is needed to produce the centripetal force in the turn you need to increase the airspeed, if you increase the AoA you will no longer be at the best Lift to drag ratio so airspeed is what is increased. Since load factor increases in the turn you will get an increase in Vs, this increase in airspeed will prevent the aircraft from reaching the stall speed.

Thoughts?
 
OneNineHundy said:
I think I have got my head around it. I will start ff by revising the forces in the steep turn. Lift is proportional to AoA and airspeed. In a level glide you fly at the speed for the best Lift to drag ratio. Therefore to increase the lift force which is needed to produce the centripetal force in the turn you need to increase the airspeed, if you increase the AoA you will no longer be at the best Lift to drag ratio so airspeed is what is increased. Since load factor increases in the turn you will get an increase in Vs, this increase in airspeed will prevent the aircraft from reaching the stall speed.

Thoughts?
Click to expand...

I'm really not sure what we're talking about here. Glides after an engine failure, say?

<<Lift is proportional to AoA and airspeed.>>

Well, yes, but that's not useful information. Lift = Weight in unaccelerated flight and weight isn't a variable. Thus, AOA determineds airspeed.

When there is an acceleration, then Lift = load factor * weight. The load factor is determined by your bank angle, n= 1/cos(bank angle).

<<In a level glide you fly at the speed for the best Lift to drag ratio.>>

You can't glide in level flight, you must mean "straight flight" ? And gliding at L/D Max is only necessary if you want to maximize your range.

<<Therefore to increase the lift force which is needed to produce the centripetal force in the turn you need to increase the airspeed, if you increase the AoA you will no longer be at the best Lift to drag ratio so airspeed is what is increased.>>

That's true. Of course, the pilot doesn't have to worry about increasing lift, because the airplane will do that for him.

<<Since load factor increases in the turn you will get an increase in Vs, this increase in airspeed will prevent the aircraft from reaching the stall speed.>>

Well, yes, but you already said you were going to keep the AOA the same, so you're just saying the same thing here.

I agree that you will keep your drag to a minimum during turning flight by letting your airspeed increase, as it must if you keep your AOA the same. It's not clear to me, though, that maximizing your range is very important when you're engaged in turning flight, rather than a straight glide.
 
All very good points tgrayson. I had this explained to me by a very experience instructor, perhaps I misunderstood what he was saying. It too did strike me as odd that we would care about the lift to drag ratio if we are turning, because range doesn't matter. Yes sorry I did mean straight glide not level glide. The reason the student is taught the steep glide is to descend in a confined space. By having no power you will have a reduction in airspeed which will increase rate of turn therefore reducing the radius.

Back to the drawing board, i'm starting to feel like a retard, all other aspects of the study is going great but for some reason I can't find a good way of explaining this.
 
OneNineHundy said:
All very good points tgrayson. I had this explained to me by a very experience instructor, perhaps I misunderstood what he was saying. It too did strike me as odd that we would care about the lift to drag ratio if we are turning, because range doesn't matter.
Click to expand...

Ask him. Perhaps there is a good reason that I can't think of. (I'd argue that minimum power is a best airspeed, because that minimizes altitude loss while turning around.)

OneNineHundy said:
By having no power you will have a reduction in airspeed which will increase rate of turn therefore reducing the radius.
Click to expand...

The lack of power will not affect turn radius, it merely affects the descent rate while turning. Airspeed and load factor are the only two things which determines turn radius in a particular airplane.

OneNineHundy said:
Back to the drawing board, i'm starting to feel like a retard, all other aspects of the study is going great but for some reason I can't find a good way of explaining this.
Click to expand...

You're trying to synthesize a bunch of technical information into an intuitive explanation and that isn't easy.
 
You must log in or register to reply here.
Back
Top